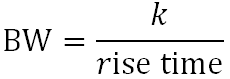在电子设计实践中，示波器是用于分析和定位问题必不可少的设备。随着电子学的发展，信号速度越来越高，利用示波器测量信号的上升/下降、建立/保持时间，过冲/下冲，眼图等参数，可以快速地定位问题。本文就示波器选型的一些关键参数作简要介绍。

带宽

所有示波器都会在较高频率时出现低通频率响应衰减。带宽的定义是指信号经过示波器/探头输入通道，幅度衰减至原幅度-3dB点的信号频率值。-3dB是基于对数标度，换算过来大概70.7%，-3dB即信号能量衰减至初始能量一半的点。

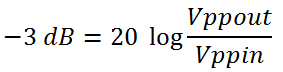
-3dB意义

举例说，假定一个幅度1V，频率100MHz的正弦信号输入到带宽100MHz的示波器，则经过示波器输入通道后，示波器接收到的信号幅度只有0.707V。

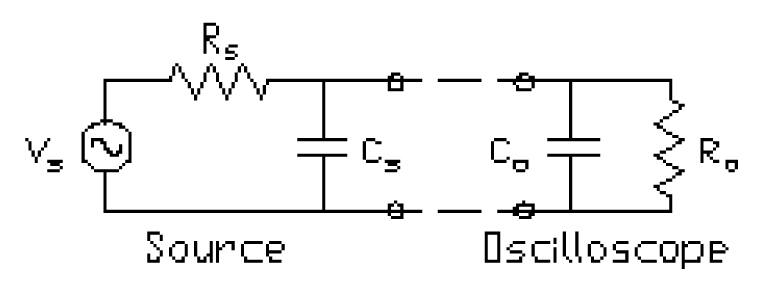
图1. 示波器和测量电路的简单模型

不同带宽指标示波器的频率响应特点

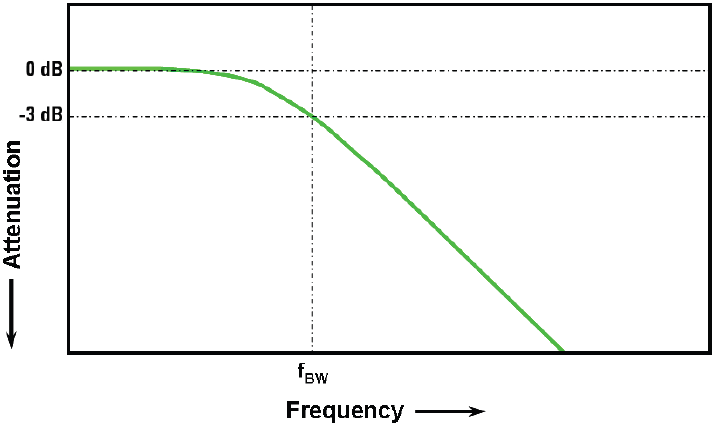
大多数带宽技术指标在 1 GHz 及以下的示波器通常会出现高斯响应，并在 -3 dB 频率的三分之一处表现出缓慢下降特征，如图2所示：

图2. 示波器高斯频率响应

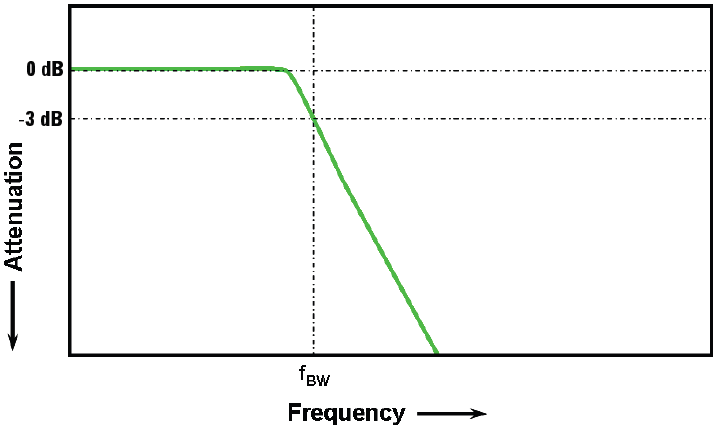
带宽技术指标大于 1 GHz 的示波器通常拥有最大平坦频率响应，如图3所示。这类响应通常在-3 dB 频率附近显示出具有更陡峭的下降特征、更为平坦的带内响应。

图3. 示波器最大平坦度频率响应

不同的示波器频率响应各有其优缺点。具有最大平坦度响应的示波器衰减带内信号的数量少于具有高斯响应的示波器，这表明前者能够更精确地测量带内信号。带有高斯响应的示波器衰减带外信号的数量少于具有最大平坦度响应的示波器，这表明在相同的带宽技术指标下，前者拥有更快的上升时间。有时，将带外信号衰减到更高的程度可有助于消除会造成采样混叠的高频率分量，从而达到奈奎斯特标准。奈奎斯特采样定律将在后文阐述。

理论误差

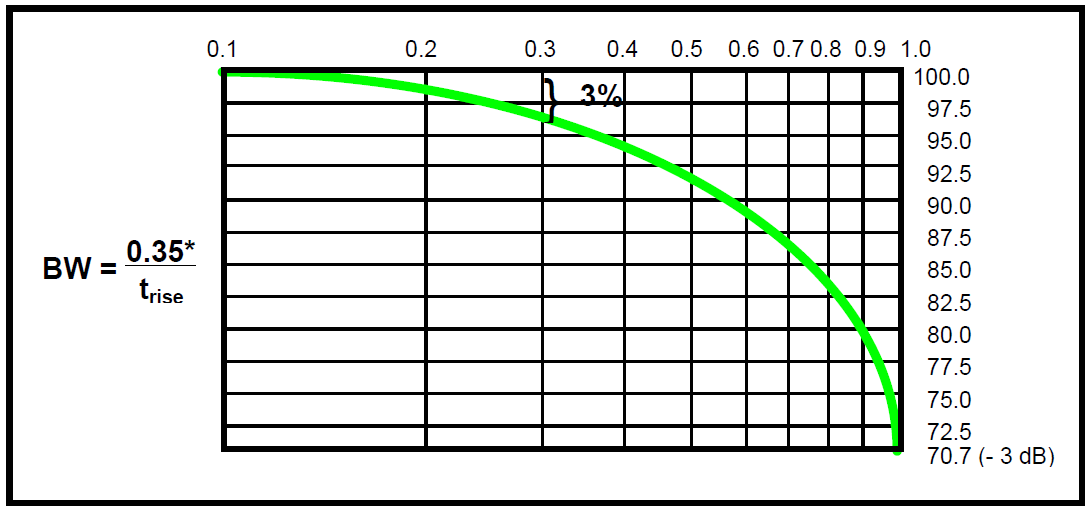
正弦波是单一频率的，使用正弦波信号发生器，在扫描频率上测试示波器的带宽和频率响应。信号-3 dB频率处衰减约为-30%幅度误差，如图4所示。所以当信号的主要频率接近示波器的带宽时，很难对信号进行非常精确的测量。理论上，测量的信号幅度误差可以用下面公式估计：

其中：R=带宽/输入信号频率

图4. 示波器带宽vs信号频率

理想方波

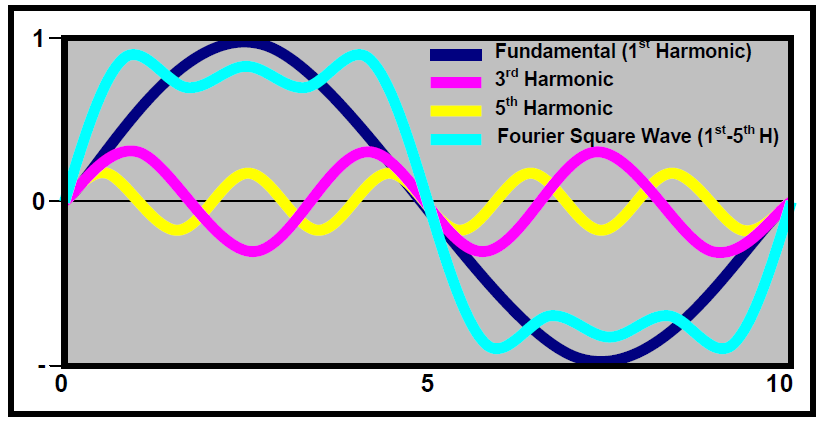
除正弦波外，其它波都可以看作不同频率正弦波加权叠加而成。方波是由基波与无数奇次谐波叠加所构成。方波是理想波形，我们近似方波只用前几个谐波叠加，叠加的奇次谐波频率越高，实际波形的上升波形越陡峭，就越接近理想方波。

图5. 方波由奇次谐波叠加构成

上升时间

信号的上升时间定义为信号幅度由10%升到90%经历的时间（也有定义20%到80%），由前面的介绍可以知道，上升时间越小，则信号叠加的奇次谐波频率越高。

对于上升时间的测量，建议示波器的上升时间是待测信号上升时间的1/3~1/5以保证足够的测量精度。理论上测量到上升时间（Trm）可以通过以下公式计算：

其中，Trd是示波器上升时间，Trs是待测信号的上升时间。

示波器的上升时间并不是示波器可以精确测量的最快边沿速度。假定输入信号具有理论上无限快的上升时间 (0 ps) 时，示波器的上升时间是示波器可能产生的最快边沿速度。虽然这个理论上的技术指标是不可测量——因为脉冲发生器实际上不能生成无限快的边沿——但是可以通过输入边沿速度比示波器上升时间技术指标快 3 到 5 倍的脉冲信号，来测量示波器的上升时间。

根据以往经验，示波器带宽应比被测系统的最快数字时钟速率高少至5倍。如果示波器满足这一标准，则其能够捕捉高达5次的谐波，并实现最小的信号衰减。这个信号分量对于确定数字信号的总体波形非常重要。但是如果您需要对高速边沿进行精确测量，要注意到此公式不会考虑快速上升沿和下降沿中嵌入的实际最高频分量。更精确地确定带宽的方法是确定数字信号中出现的最高频率，而非最大时钟速率。最高频率是由设计中的最快边沿速度决定的。也就是说，带宽和上升时间直接相关。通常，上升时间和带宽（BW）的关系如下：

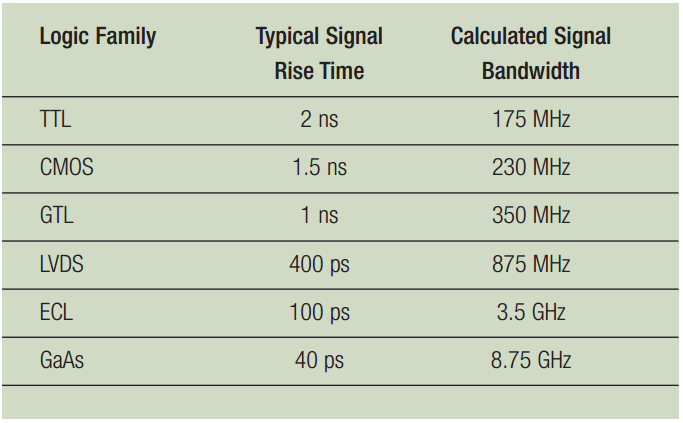
根据示波器不同的频率响应特点，带宽小于1GHz的高斯响应示波器的k值一般取0.35，带宽大于1GHz最大平坦度响应示波器的k值在0.4到0.45之间。表1列出常见逻辑电平不同上升时间对应的带宽选择。

表1. 部分逻辑电平上升时间/带宽估计

采样率

采样率指的是示波器的ADC采样模拟信号的速率，和示波器带宽没有直接联系。采样率的单位Sa/S表示每秒采样的次数。决定示波器采样率的是控制ADC转换单元的时钟频率。采样率越高，采样的波形越完整，越容易捕捉到更丰富的波形信息。有的测量需要长时间观测波形信息，这时应该选择低采样率的示波器，因此最小采样率也可能是选择示波器的一项考量因素。

图6. 采样示意图（实时采样）

根据Nyquist采样定理，当对一个最高频率为f 的带限信号进行采样时，采样频率必须大于f 的两倍以上才能确保从采样值完全重构原来的信号。这里f称为Nyquist频率，2f为Nyquist采样率。对于正弦波，每个周期至少需要两次以上的采样才能保证数字化后的脉冲序列能较为准确的还原原始波形。如果采样率低于Nyquist采样率则会导致混迭（Aliasing）现象。

奈奎斯特采样定理

对于最高频率是f的带限信号，等时采样频率必须大于2倍f，才能保证原始信号得以无混迭、唯一地重构出来。

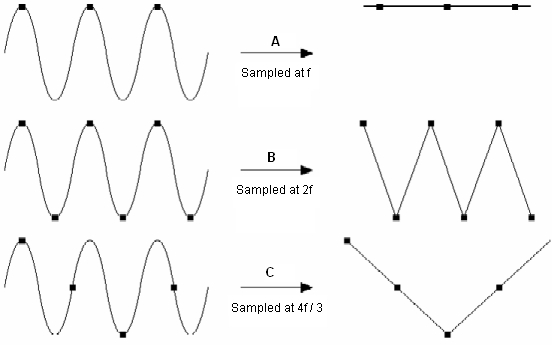
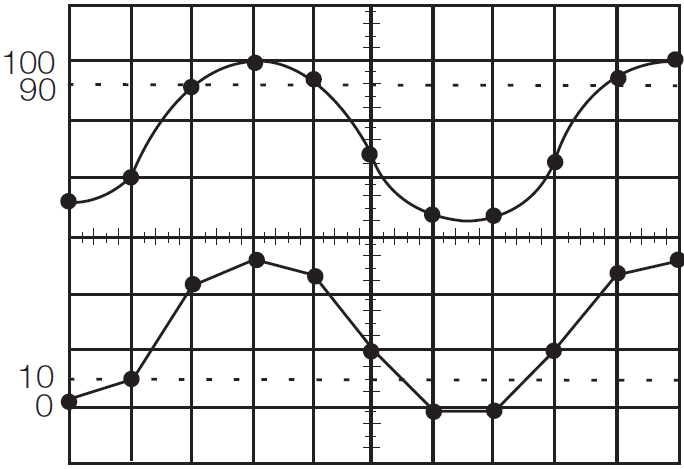
图7表示了在不同采样率下恢复出来原始信号的波形。当采样频率等于信号频率f时，重构的信号为DC直流电平；当采样频率上升到2f时，恢复出来的信号和原始信号具有相同的频率，但信号表现为三角锯齿波。将采样率增加到一定范围，比如5f，就可以比较准确地重构原始信号了；图7示C情形，此时Nyquist频率为(4f/3)/2 = 2f/3，小于信号频率f，因此采样恢复出来的原始信号是不准确的混迭的信号。

图7. 不同采样率恢复出来的原始信号

混迭信号频率可以通过以下公式计算：

混迭频率=绝对值（N*采样频率– 原始信号频率）

其中，N取整数，取值满足（N*采样频率）最接近原始信号频率。

实时采样和等效采样

示波器主要有两种采样方式：实时采样和等效时间采样（等效采样）。等效采样进一步可分为两类：随机等效采样和顺序等效采样。每种采样方式有各自的优缺点，对应着不同的应用领域。

实时采样

实时示波器有时也称为“单次”示波器，它在每个触发事件上捕获一个完整波形。也就是说，它在一个连续记录中捕获大量的数据点。为了更好的理解这种数据采集类型，我们将实时示波器假设为一个速度极快的模数转换器（ADC），其中采样速率决定采样间隔，存储器深度决定要显示的点数。实时采样是获得快速瞬时波形的唯一方法。为了捕获任何波形，ADC采样速率要明显快于输入波形的频率。另外，实时示波器瞬间大量的采样值必须立即存储到示波器的内存，这也对示波器的设计提出了挑战。实时采样示波器采样速率可以达到40GSa/s，决定了带宽目前可扩展到13GHz。

实时示波器可以根据数据本身的特性进行触发，通常输入波形的幅度达到一个特定阈值时，触发就会发生。示波器此时开始以异步速率（与输入波形的数据速率没有任何关联）将模拟波形转换为数字数据点。示波器对输入波形的幅度进行采样，并将这个幅度值存储到存储器中，然后继续下一个采样（如图8所示）。触发的主要工作是为输入数据提供一个水平时间参考点。

图8. 实时采样

等效采样

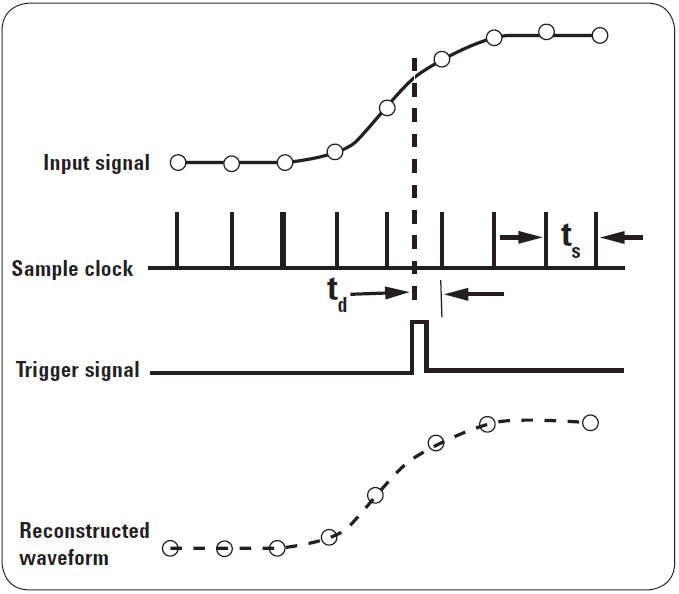
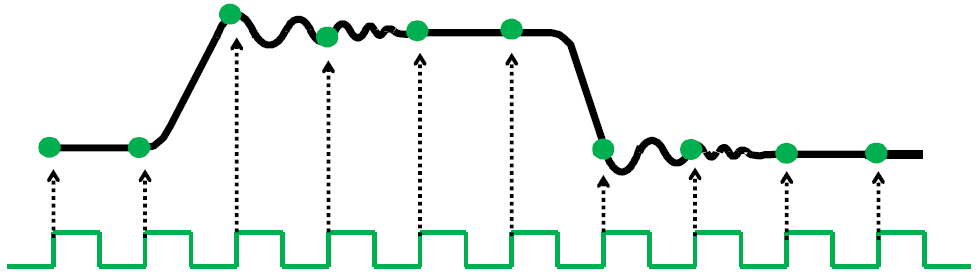
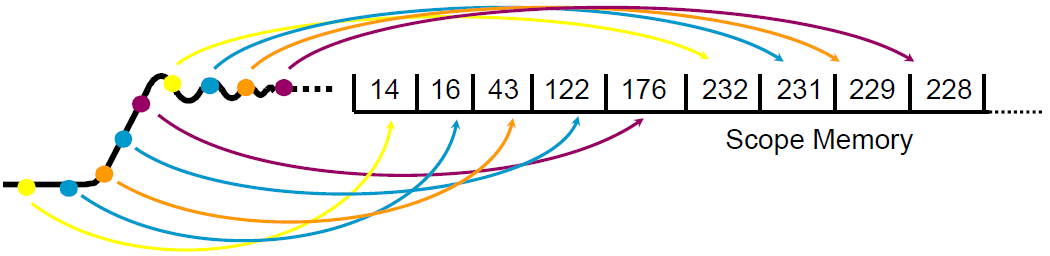
在测量高频信号时，示波器可能在一次扫描中无法捕获足够的采样点。当待测信号频率大于示波器采样率的1/2时，可以选择等效采样示波器。等效采样仅测量采样瞬间波形的瞬时幅度。与实时示波器不同，等效时间采样示波器的每次触发只对输入信号采样一次。下次触发示波器时，会增加一个小小的延迟然后进行下一个采样。预期的采样数决定重新生成波形所需的周期数。等效采样仅对重复信号有效，通过大量在不同时间点/相位的采样值，重构信号的完整波形，如图9所示。

图9. 示波器通过等效采样获取高频重复信号波形

等效采样示波器，所谓等效，是指用较低的实际采样速率（500Sa/s）获取的信息量与较高采样速率（1000Sa/s）获取的信息量是等效的，代价是获取相同信息的时间变长了。等效采样降低了实际采样速率，减小了单位时间内的采样点数，降低了对数据存储速度和容量的要求。

等效采样有两种方式：随机等效采样（Random equivalent-time sampling）和顺序等效采样（Sequential equivalent-time sampling）。

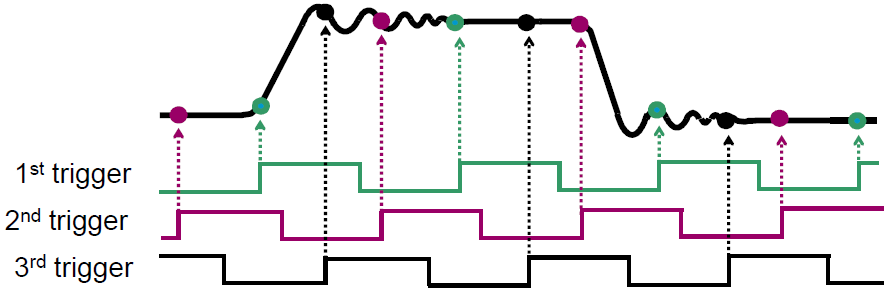
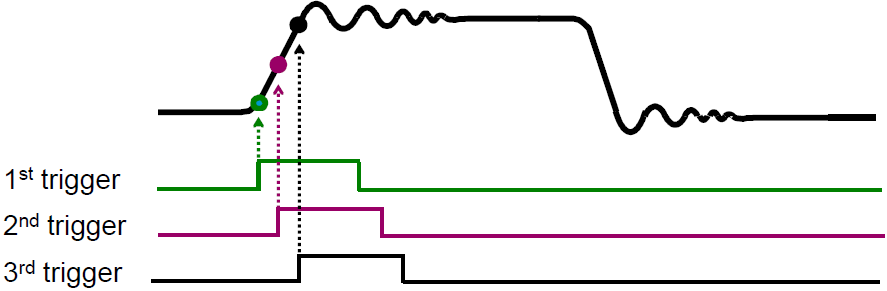
随机等效采样的第一组采样点是在随机时刻采集的，而与触发事件无关，这些采样（第N组）点是基于示波器内部时钟的，与测试信号无关。当示波器在等待触发事件到来时，其内部就在连续地采样并将结果存储起来。当一个触发事件到来时，示波器内一个定时系统就从这个时刻开始数据的采样直到下个触发事件开始下一组数据的采样。由于采样间隔是固定的，示波器能够据此计算出所有采样点在存储器中的位置。当第一次采集所有的采样点存储完毕以后，就开始采集一组新的采样点并等待新的触发事件，新触发时间到来以后，计时系统进行新的时间测量并计算出这些新的采样点位置，这些新采样点落在第一次采样点之间未填充位置，用这种方法，测量的波形由X轴上随机位置出现的一组组采样点构成。随机等效采样的过程如图10所示。

在同样的采样率下，使用随机采样方法填满一个完整的波形记录所消耗的时间比顺序采样多很多，因为这时是用统计的方法来填充所有存储器位置的。随机采样技术的优点在于可以提供预触发信息以及触发后信息。

图10. 随机等效采样

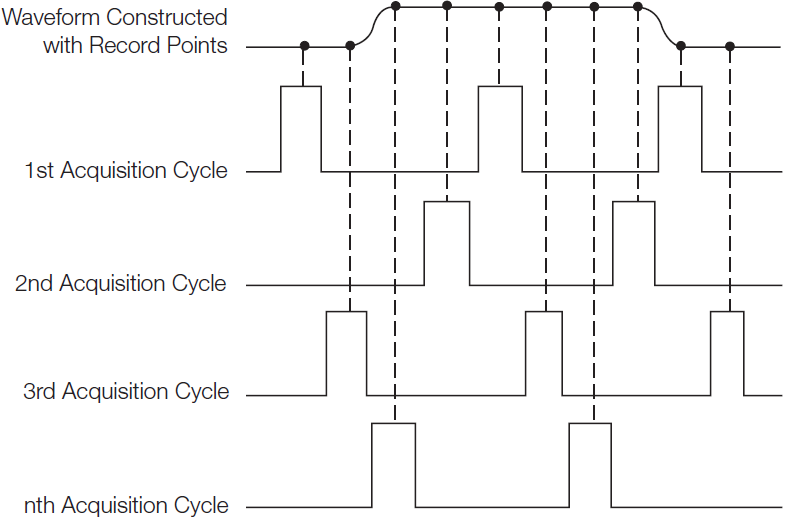
顺序等效采样，采样点的采集是按一个固定次序进行的，即在屏幕上以从左往右进行采集，每到来一个新的触发事件就采集一个采样点。为了填满一个完整的波形记录，记录中有多少个存储位置就需要多少个触发事件，如图11所示。第一个触发事件到来后就立即采集第一个采样点，并将其存入存储器，第二个触发事件则用来启动一个定时系统，此定时系统将产生一个很小的时间延迟Δt，经过这个Δt的延迟时间后，再采集第二个采样点。第三个触发事件到来后，该定时系统则产生2Δt的延迟时间。此延迟时间以后再采集第三个采样点，并以此进行下去。

这就是说第N个新的采样点的采集是在相对于第一次触发事件延迟了（N-1）Δt的时间后进行的。其结果是示波器上显示的波形是由按固定次序出现的采样点而构成的。即第一个采样点在屏幕的最左边，接着各采样点依次向右构成显示波形。

在顺序采样模式下，采集波形的周期数，即触发事件数等于存储器的记录长度。顺序采样可以实现后触发延迟功能，但是不能提供预触发信息。在快速时基设置下，填满一个存储器记录所需的时间是很有限的。其速度比随机采样要快得多。

图11. 顺序等效采样

关于实时采样示波器和等效采样示波器各自的优势，在Agilent的应用指南《等效时间采样示波器和实时示波器的差别》中提到：

实时示波器的优势

可以显示单次瞬时事件
无需显式触发
无需重复的波形
直接测量周期到周期抖动
长记录长度/ 深存储器
适用于故障诊断情况

等效时间采样示波器的优势

更低的采样速率支持更高分辨率ADC转换
更宽的带宽
更低的本底噪声
更低的固有抖动
可以包括前端光学模块
可以用于TDR以获得阻抗测量和S参数测量
能够以更低的成本获得解决方案

插值法

示波器根据采样点的值恢复原始波形，由于采样的数据是一些离散点，这时候需要通过插值法将这些离散点连接在一起，构成连续的波形。通常使用的插值法有线性插值法（Linear Interpolation）和正弦插值法（Sinx/x Interpolation），线性插值法将采样的离散点直接连接，仅限于重构那些直角边缘的方波信号；而正弦插值法通过数学运算填充离散点之间的空隙，得到的波形接近曲线，更符合实际情况。正弦插值法多应用于采样率是带宽3-5倍的场合。便于精确测量和重构波形，采用正弦插值法示波器的采样率至少为信号最高频率的2.5倍，采用线性插值法示波器的采样率至少是信号最高频率的10倍。有些示波器可以由用户选择何种插值法重构波形，比如用线性插值法重构方波、脉冲波形，使用正弦插值法重构正弦波。图12表示不同插值法恢复波形的情况：